Harbor or terminal tugs are excellent candidates to achieve significant reduction in costs, pollutants and fuel consumption through electrification. This is because traditional diesel tugs have engines sized for full bollard pull, which is used for only around 7 percent of the time. For most of the operation time, the main engines are operated in idling mode. Carloyn Dorothy, built in 2009, now operating in the ports of Long Beach and Los Angeles, was the first practical demonstration of electric tugs. However, as pointed out by experts, the transformation of the industry to electric/hybrid vessels will not take place overnight and requires research and development to get the full value of additional cost investments made in ship design, equipment and construction. This requires funding, but prototype construction is a sticking point for most tug owners. Therefore, Nanyang Technological University has partnered with ABB Pte. (Singapore) Ltd. to analyze the design of harbor tugs equipped with the Onboard DC Grid, mathematically model them and simulate their response in a MATLAB/Simulink software environment. The purpose of this investigation was:
- To investigate the ideal investment in equipment and design of harbor tugs equipped with Onboard DC Grid in order to provide a return on investments through fuel and operational cost savings within a fixed time horizon.
- To find the power management schedule of diesel engines and batteries for a given design of harbor tug equipped with Onboard DC Grid that achieved the maximum operating cost savings.
This article describes the modeling strategy overview used to develop the programmed mathematical model in MATLAB/Simulink, which is later used to investigate both the ideal design and optimal power management strategy. The mathematical model accounts for response of components such as diesel engine generators and batteries to meet the load demand. This model is later used, with the optimization toolbox available in MATLAB/Simulink, to evaluate the optimal solution to both the ideal design and power management strategy problem, and the key conclusions are presented.
The solution of the optimal design formulation recommends that a tug equipped with Onboard DC Grid can provide a return on investment within five years. Significant fuel savings are achieved using the Onboard DC Grid configuration over the traditional mechanical configuration. The optimal solution recommends using both batteries, as well as multiple smaller sized diesel engine generators, instead of a single large diesel engine generator used on a purely mechanical tug. However, the battery size recommended is much smaller, compared with the installed diesel engine capacity, indicating that most of the benefits associated with hybrid battery/engine configuration can be achieved through a relatively small investment in the batteries. The schedule of engines and batteries can be easily solved after formulating the optimal power management problem if the load demand profile is known. However, the exact load profile is usually not known. Only the general characteristics of the load demand can be deduced based on the location and jobs serviced by the tug. A novel but simple strategy to predict the load demand from historic load measurement data and general operational characteristics of the tug is proposed. This is integrated with the optimal power management formulation to determine the schedule of engines and batteries for the Onboard DC Grid-based tug.

Figure 1 Schematic of power distribution system of a tug equipped with Onboard DC grid 
Figure 2 Simulink model for power distribution system of a tug equipped with Onboard DC grid
Mathematical modeling of a tuq equipped with Onboard DC Grid
A schematic of the drive-train model for a tug equipped with Onboard DC Grid is shown in Figure 1. In general, a hybrid electric configuration of a tug can have several diesel engine generators and batteries connected to a DC bus that are managed by an “intelligent” distribution system regulating the power output and running the schedules of each engine and the batteries in response to the load demand.
Based on the basic architecture of the power distribution system presented in Figure 1, it is possible to program a mathematical model that simulates the response of diesel engines and generators at different levels of fidelity. For example, it can be assumed that the diesel engine generators and batteries can respond instantaneously to reach their power set-points, that is, the transient dynamics of engines and batteries are neglected. As such, this is a reasonable approximation in practical applications of electric tugboats, where the engines and batteries are controlled via their integrated controllers to reach their power set-points in seconds and milliseconds, respectively. Thus, the duration of transient response is much smaller than the working durations for the engines and batteries at each specified set-point, which can be several minutes. Figure 2 provides an overview of a relatively higher fidelity model programmed in the Simulink environment in MATLAB software, wherein the transients of diesel engines and the controller response characteristics are accounted for to provide an accurate estimate of fuel consumption, as well as loss of power at different components due to their individual efficiencies. It should be noted that the higher the fidelity of the model, the more computation power is required to evaluate the response of the system. This can become an important concern when evaluating the ideal design solution of an electric tugboat or determining the optimal power management scheme, as these problems require evaluating the response for several possible candidate scenarios. Such repeated evaluation of candidate scenarios can easily cascade the computation burden.
In the steady state model for the power distribution system, where the transient dynamics of diesel engine generators and batteries, as well as the controller response time, are neglected, the important characteristic of the system response modeled is that the power output from diesel engines and batteries must be greater than the load demand. This is necessary for the tug to fulfill the assigned job. The other aspects of the model are similarly modeled irrespective of the chosen fidelity level for the tug model. These aspects include a set of rules that determine when engines should be switch on or off and whether the batteries are in charging or discharging mode, engine-generator efficiency with respect to its operating conditions and the load demand characteristics. Thus the aspects of the power distribution system of the Onboard DC Grid-based tug that need to be modeled for the general case shown in Figure 2 are as follows:
Control loop for diesel engine generator
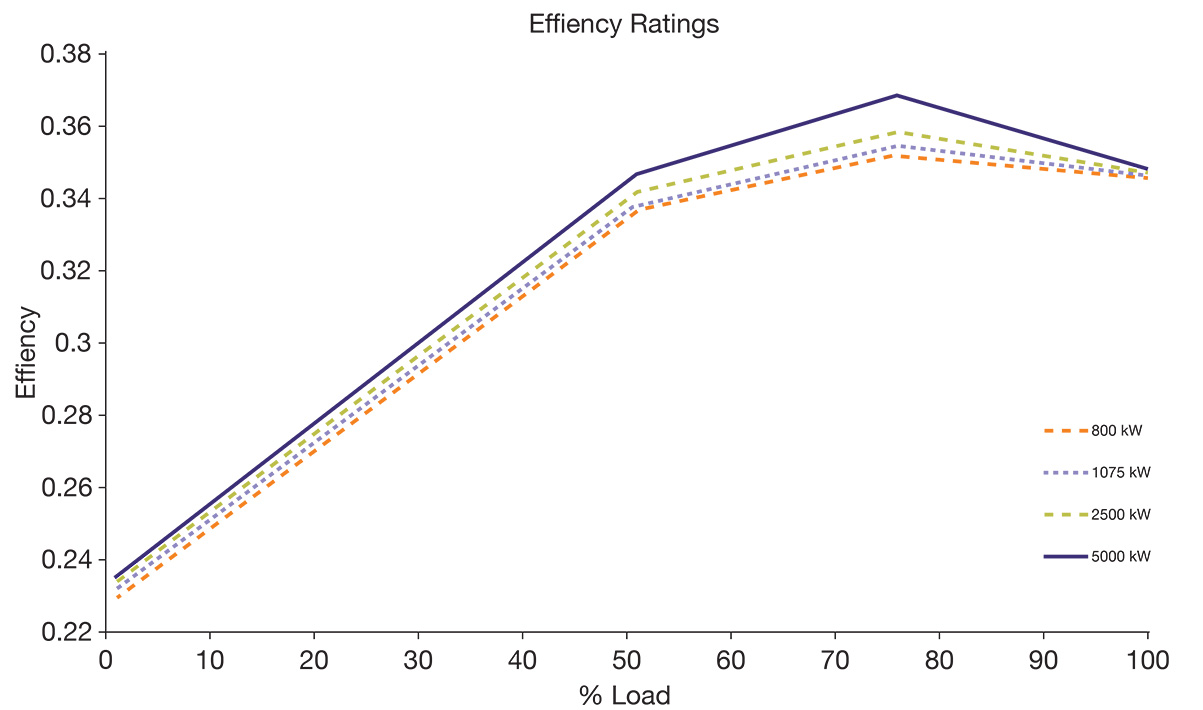
Diesel engine generator power output is regulated by a PID controller. The control takes in the error of the DC bus voltage from the nominal bus voltage as input. Usually the dynamics of diesel engine generator are represented by a first order transfer function in Laplace domain or as a rate limiter in time domain to simulate the lag in the pickup response. Figure 3 describes the efficiency characteristics of a diesel engine. The efficiency of a generator is relatively less sensitive to changes in operating speeds and thus can be assumed as constant. Usually, marine generators can have efficiencies of around 95 percent in such operating conditions. Therefore, the overall efficiency of the engine generator set is the product of these two efficiencies. It can be seen that the engine has a sharp peak in efficiency in a narrow operating region at around 70 to 90 percent of the rated load. The hybrid tug configuration decouples the demand load with engine operation. This allows the engine to run in generally optimal conditions, which is the main reason for improvements in fuel efficiency from such systems.
Control loop for batteries
Marine applications usually use battery arrays or battery packs. A battery array can contain several battery packs, each of which consists of several modules. However, for improved battery life and utilization, the load is distributed equally among all battery modules, such that each of them is at the same state of charge (SOC), which is the parameter used for describing the stored energy in the batteries at a given time. The batteries assist by smoothening the power demand requirements from the diesel engine generators that allow them to operate highly efficiently. Compared with diesel engines, the batteries’ response is faster and is assumed instantaneous in this work. Some power losses can occur in batteries as well, which are approximated as a quadratic function of the battery supply power. However, usually such these losses are much lower than in diesel engine generators, and may be ignored.
Power management controller
The power management controller determines when an engine needs to switch on or off, and if the batteries need to charge or discharge. Later in this article, the described model of tug equipped with Onboard DC Grid is used for evaluating the optimal design and schedule for running engines and batteries, as well as
Load demand profile
This work considers a typical operational load profile of a harbor tug as was provided by ABB Singapore and is presented in Figure 4. The low-load demand occurs for around 65 percent of the overall operating cycle and requires only around 10 percent of the rated power, while the medium-load demand occurs for around 20 percent of the operating cycle, requiring around 30 percent of the rated power. The high-load demand takes 15 percent of the operating cycle that requires around 90 percent of the rated power.
According to the operational characteristics of the typical harbor tugboat, this work assumes a tug subject to the load profile depicted in Figure 5. The rationale for the chosen load profile is that when the job is first assigned, the tugboat needs to be driven to reach the target and thus is in the loitering/slow steam mode. After reaching the designated work area, the tugboat waits for some time before starting its task, during which the auxiliary systems will continue to run. The power requirements during this waiting period are similar to those at the quay. The power demand during servicing is usually higher and includes assisting at medium-load (low assist) and high-load (high assist) demand. Lastly, another period of loitering/slow steaming is required for the tugboat to go back to its station.

Figure 4 Load profile of a typical harbour tugboat 
Figure 5 Load profile demand used in optimization formulation
Optimization of a tug design equipped with Onboard DC Grid
In general, an optimization problem is formulated as:
min J(x) subject to G(x)≤0
The cost function J(x) takes into account the different trade-off costs that a tug owner may encounter during investment in and operation of the Onboard DC Grid-based tug. The constraints G(x)≤0 represent the physical system limitations or design limitations imposed by practical considerations. The physical system limitations are inherently captured by the mathematical model of a tug equipped with Onboard DC Grid that was presented in the previous section. MATLAB software has an optimization toolbox containing standard optimization routines, including the genetic algorithm routine, which was used to evaluate the solution in this case. The advantage of using MATLAB/Simulink is that both the system constraints specified using the Simulink model, as well as additional design and practical constraints, can be programmed and considered during the evaluation of the optimized solution.
Problem formulation for design optimization
For selecting a given design configuration, the tug owner must consider the upfront equipment and manufacturing cost of a tug, as well as the fuel and maintenance cost distributed over the operational life cycle. Thus, the cost function for the optimization problem was formulated to have three terms as:
J = w1 x Equivalent Equipment Cost + w2 x Design Cost + Fuel Consumption Cost
where equivalent equipment cost accounts for equipment purchase and maintenance, and the design cost accounts for cost associated with the space requirements of the installed power distribution system. These costs are a function of the various diesel engine generator and battery pack candidates considered in a tug design. Each candidate is defined by the equivalent equipment/maintenance costs, space requirements and power rating. The weights w1 and w2 allow for flexibility to put more emphasis on certain costs than others, as is often dictated by practical considerations. For example, w1 and w2 may be selected to be greater than 1 if upfront costs need to be penalized more or less than 1 should the regulations require reduced emissions, which can be translated to less fuel consumption.
Besides the system operation constraints that are inherent in the Simulink model, additional design constraints that arise from practical considerations are also modeled. For example, classification societies require that the total installed engine capacity be more than the rated power of the tug, and the DC bus voltage should be within a nominal narrow band for proper functioning of installed equipment.
Results of design optimization
The optimization formulation for the tug design problem presented so far was simulated to determine an optimal design for a tugboat. The fuel costs were calculated over five years assuming repeated operating cycles of 90 minutes each, with six cycles per day. Figure 6 provides the optimal solution picked up by the genetic algorithm routine, which recommended using three small engine generators of 800 kW, two medium engine generators of 1075 kW and 22 modules of batteries, each of 6.5 kWh capacity. It is noteworthy that small engine generators are preferred over larger engine generators of 2500 kW. Using small engine generators allows switching of the engines sequentially, such that for most operating conditions the running engines are operating at near optimal conditions. Further, it can be seen that the battery capacity recommended is very small, compared with the engines. This indicates that even a small battery capacity can provide significant improvement in efficiency through load smoothening of engines. However, as the battery capacity is increased further, the efficiency improvement achieved is not significantly high enough to justify the cost of additional battery investment.
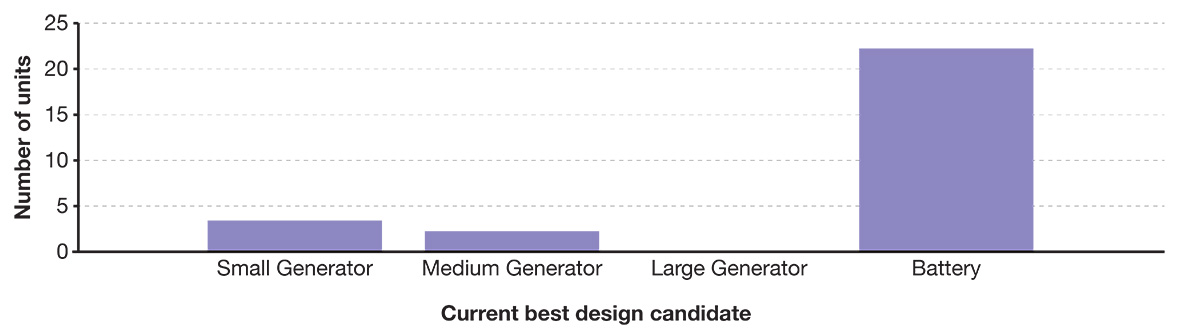
Table 1. Cost breakdown for the optimal design and corresponding efficiency
| COST COMPONENT | COST ($) | |
| OPTIMAL ELECTRIC TUG | MECHANICAL TUG | |
| Equivalent Equipment Costs | 3,059,000 | 2,813,333 |
| Design Costs | 320,736 | 126,945 |
| Fuel Consumption Costs | 10,642,000 | 13,207,000 |
| Efficiency | 33.15 percent | 31.59 percent |
Table 1 compares the costs incurred by the recommended optimal design candidate with respect to the mechanical tug configuration. It can be seen that while additional investments are required in equipment and design, costs are recovered in fuel savings through improvement in efficiency. Also, it must be noted that the fuel consumption cost and efficiency improvement is based on a simple rule-based power management system described in the previous section. However, in the next section, we describe how to intelligently switch on and off the engines and utilize the batteries. The implementation of such power management systems should provide even more fuel savings and efficiency improvements, which could make the Onboard DC Grid equipped tug an even more attractive option.
Optimization of electric tugboat power management Problem formulation for optimization of power management
In the previous section, the problem formulation presented included the cost associated with manufacturing a tug of a given configuration and its operating cost. Once a tug design is finalized, the main consideration for a tug’s owner is to get the maximum mileage from the investment. This requires an intelligent use of resources on a tug equipped with Onboard DC Grid, which can result in maximum fuel savings while meeting the load demand as dictated by the tug’s operation. As in the previous optimization formulation, again, there are trade-off costs involved. For example, fuel savings can be obtained by reducing the diesel engine’s power output, but batteries may not have sufficient stored energy to meet the load demand. Even if batteries are used to meet the load demand, the stored energy needs to be finally recovered by either onboard generation or purchasing it from the grid. Thus, a new problem needs to be formulated to determine the optimal power management strategy that accounts for these cost trade-offs. The chosen cost function accounts for the fuel consumption, change in stored energy of the battery and the ability to track the given load profile as:
J = Fuel consumption + γ×SOC change + λ×Load tracking
As in the case of the previous optimization formulation, the model presented in Figure 2 can be used to describe the system operation constraints. A limitation of using the described mathematical model of electric tugboat subject to the cost function for power management is that at each time several solutions using a different combination of power outputs from engines can exist for operating at a given efficiency. Therefore, the optimization algorithm often recommends random and unnecessary power switches among different engines at each time step. Such random and unnecessary power switches are uneconomical and detrimental to the health of the system.
A typically detrimental and uneconomical solution that the optimization algorithm can recommend is when an ith engine switches from on mode to off mode, while another jth engine switches vice versa. If ni(k) represent that an ith engine is running (n = 1) or switched off (n = 0) at kth time instant, then to eliminate such redundant switches, the following conditions are set on the operation mode of each combination of different engines as:
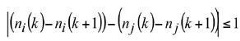
for all possible time instants k
Another similar issue can be related to frequent switching on and off of the engines. Once an engine is switched on, it is usually desirable to run it for at least a certain length of time. A start-up operation of an engine usually penalizes the fuel consumption heavily and results in more pollutant emissions, compared with continuous operation of the engine. A similar constraint can be included between different time samples to avoid rapid on-off switching of an engine between consecutive time instants as follows (assuming that ith engine is running at kth time instant):
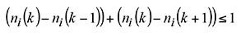
for all possible time instants k
Optimized results for power management: known load profile
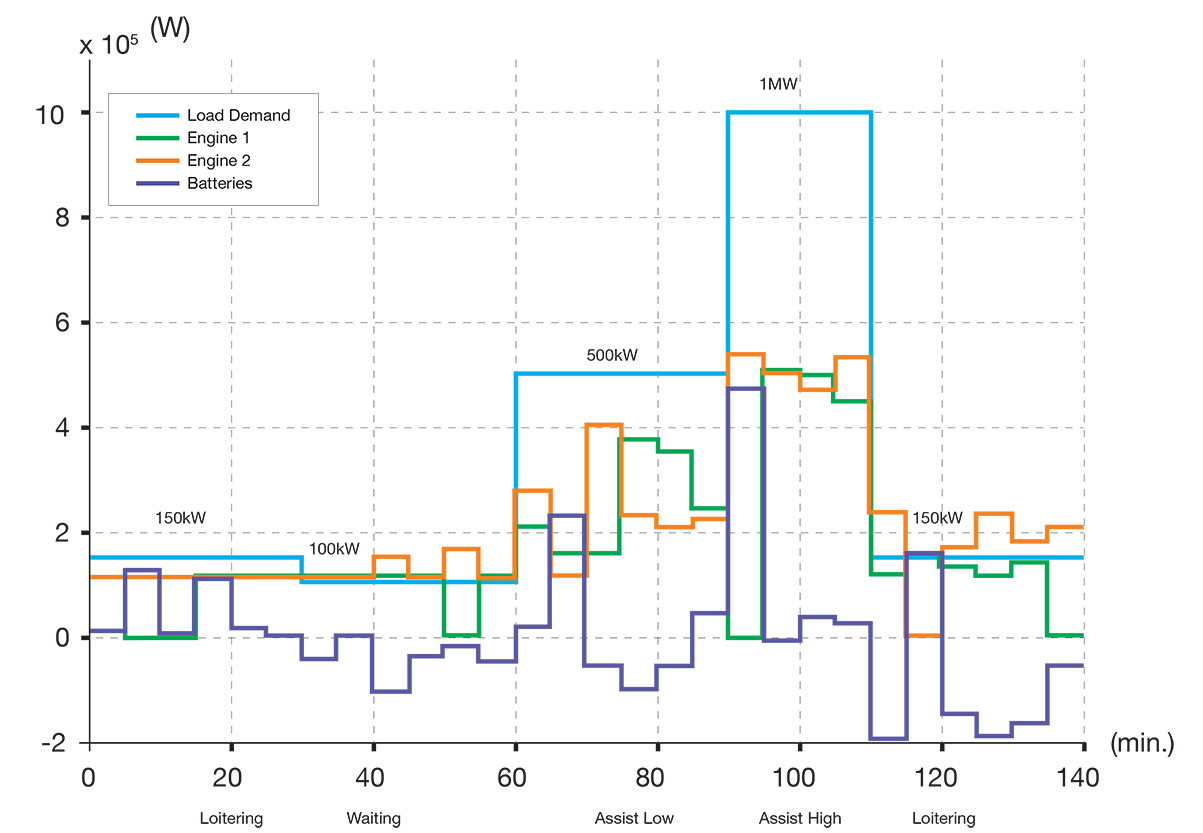
Consider an ideal case, where the operation profile of the tug is known in advance. This is similar to the case when the tug does the same task repeatedly. In this case, while neglecting small variations that may occur due to weather and waves, both the power demand requirement and the respective duration at each power demand level can be known a priori. Pre-programming for power output/operation of the engines and the batteries is then sufficient to ensure system’s efficiency. Figure 7 shows the results from optimization for a similarly known load profile (which is the same as shown in Figure 5). It can be observed from Figure 7 that the engines usually operate with higher power output in response to the load demand during the assisting modes of the tugboat, and operate at a lower power output or switched off mode to reduce fuel consumption during the low load demand periods. It can further be seen that during some operating periods, for example 5 to 10 minutes, the batteries can discharge to respond to the load demand, allowing one or more engines to turn off, which reduces the engine fuel consumption. Conversely, during some operation periods, especially observed at the end of the operating cycle for shown results, the batteries may charge to exploit the surplus power generated by the engines, which reduces the wasted power.
Optimized results for power management: unknown load profile
Generally, the exact load demand for a tug is not exactly known. However, based on the port where a harbor tug is operated, its general operating characteristics such as the relative amount of time spent in each operation mode can be deduced. A wide variety of research in load prediction is available for marine vessels and land-based vehicles, which includes artificial neural networks, support vector machine, fuzzy network and numerical methods. While these methods are effective when a lot of data from measurement and system information is available, it is not straightforward to use information about general operating characteristics of a harbor tug to predict the load and demand and optimize using the formulation presented earlier. Therefore, a novel prediction scheme, which only requires information regarding the general characteristics of tugboat operation, is proposed in this research to forecast the load demand and then combined with the optimization formulation for power management presented earlier in this section to determine the engine and battery power outputs and the engine operation schedule.
The mechanism of prediction scheme is based on the historical load profile information and the general operational characteristics of a typical harbor tug profile shown in Figure 4, that is, the low-load demand occurs for around a = 65 percent of the overall operating cycle, the medium-load demand occurs for around b = 20 percent of the operating cycle and the high-load demand takes around c = 15 percent of the operating cycle. Let us say that in an operating time interval [0, nΔt]: anΔt, bnΔt, and cnΔt were the time intervals for which the tugboat operated in low-load, medium-load and high-load demand modes respectively. Here n, an, bn and cn are integers such that an + bn + cn = n and the sequences [an]n∞=1, [bn]n∞=1 and [cn]n∞=1 are increasing. To predict the load demand in the interval [nΔt, 2nΔt], the integers a2n, b2n and c2n are identified such that:
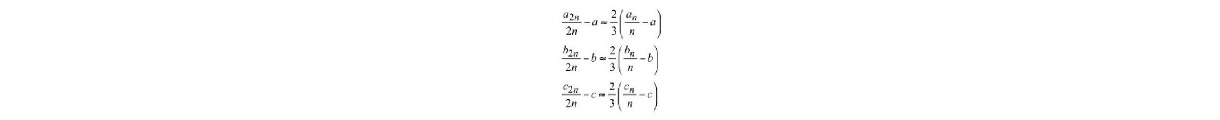
It can be verified that this prediction scheme ensure that the time percentages for which the tugboat operates in low load, medium load and high load satisfy:
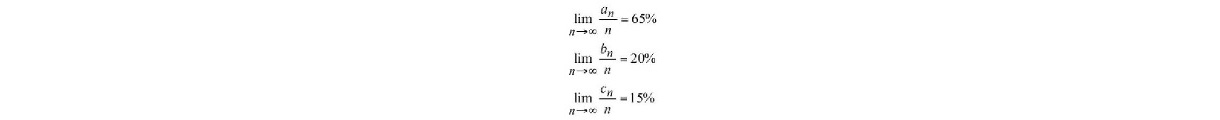
The prediction scheme can be integrated with the power management optimization to successively find an optimal power management scheme over increasing time horizons. For the first iteration, when the load measurement is not available, the general operational characteristics can be used to determine the optimal schedule for engines and batteries. After the first iteration, the load profile during this interval is known and can be used to predict the load up to twice the length of the load measurement. Thus, the predicted load from a given time instant to the subsequent time horizon can be used for evaluating the optimal schedule for engines and batteries in the next iteration. This process can be repeated until the operation cycle terminates.
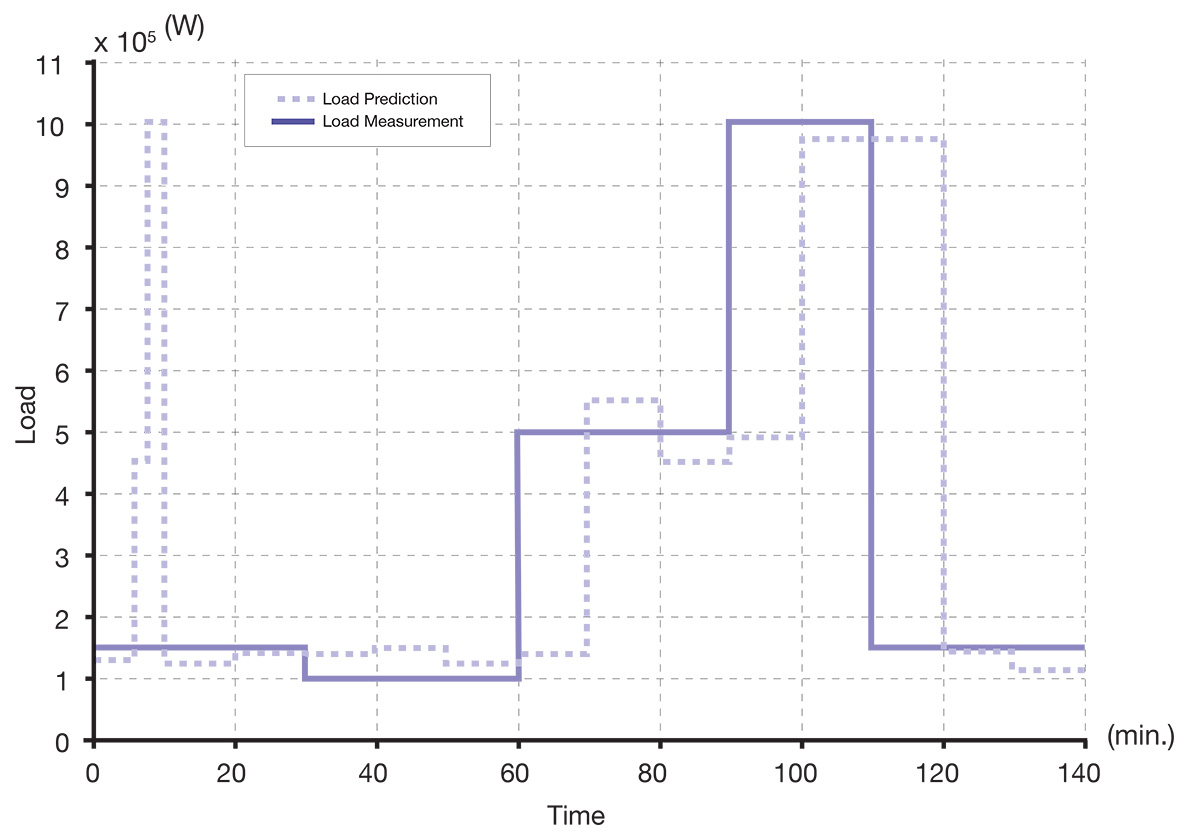
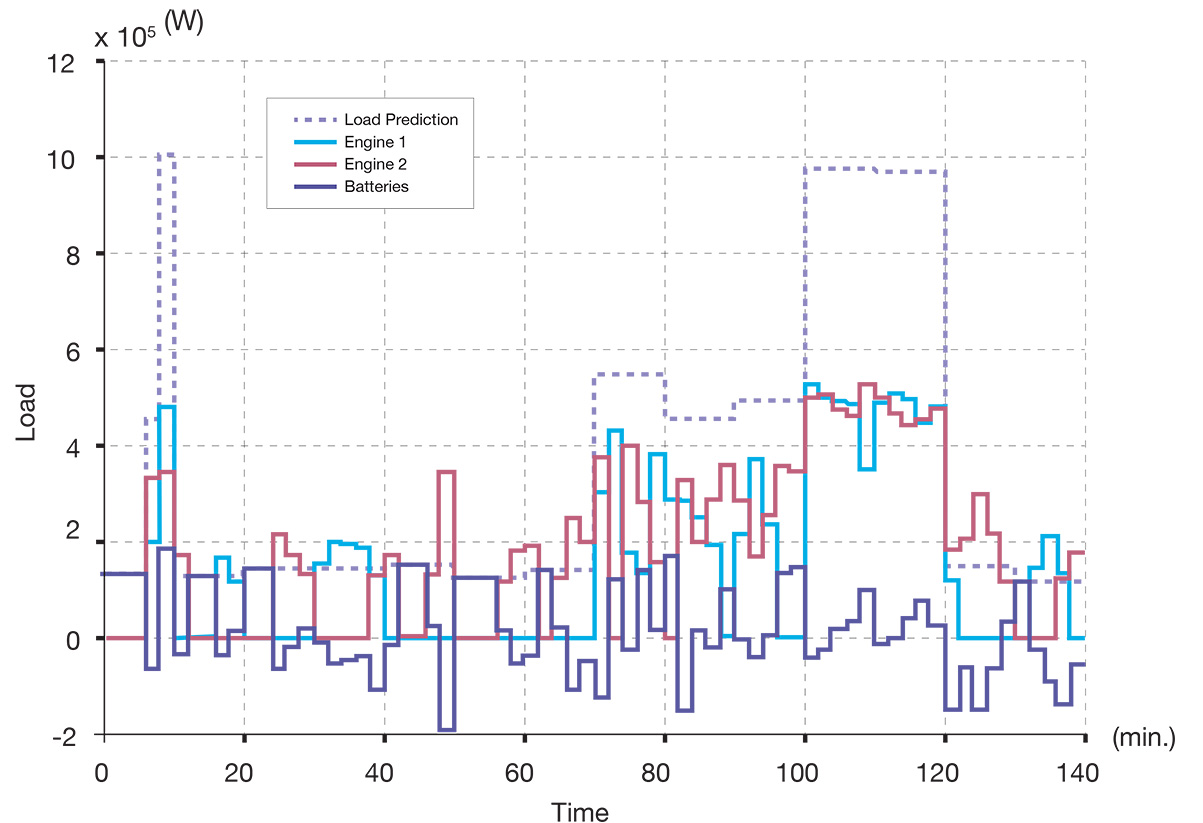
Figure 8 shows a comparison between the load prediction utilized for optimization and the assumed load measurement of electric tugboat during a 140-minute operation cycle. The prediction scheme anticipates that the tugboat operates in low-load, medium-load and high-load demand modes for around 61.4 percent, 22.9 percent and 15.7 percent of the working cycle respectively. At each iteration step, the load prediction in the subsequent time horizon of 10 minutes’ length is combined with the optimization formulation presented earlier in this section to determine a solution regarding the engine/battery power output and the engine operation schedule in that predicted horizon. The overall schedule for engine and battery power output for the entire operation cycle is shown in Figure 9. It was found that the fuel consumption in this prediction-based solution, when compared with that in the ideal optimum solution shown in Figure 7, showed an increase of 6.07 percent. This increase in fuel consumption is marginal, when compared with the benefits obtained from the use of hybrid tug configurations, which demonstrates the effectiveness of the proposed power management scheme.
Concluding Remarks
Research and development is needed to accelerate the acceptance of Onboard DC Grid and hybrid electric vessels by the marine industry. However, prototype building is expensive and is not always feasible to fully investigate the full potential of the added investment in these vessels. The research summarized in this article describes the mathematical modeling with key system considerations that the researchers at Nanyang Technological University developed with design input regarding Onboard DC Grid-based tugs from ABB Singapore. The mathematical model was programmed in the Simulink environment of MATLAB and later used for optimizing the tug’s design and power management strategy. The optimization of the tug’s design was done to determine the ideal investment in diesel engines, including the number of engines and power rating of each engines and battery packs that would provide a return on investments over a given time horizon. The costs considered in this investigation included the equivalent equipment and maintenance costs, the costs associated with space requirements of the power distribution system and fuel costs. The optimization of the power management strategy evaluated the running schedules for engines and batteries including their power output that would results in minimum operating costs. This optimization problem can be easily solved if the load demand profile is known a priori, which can be the case if the tug repeats the same operation over and over. However, usually only the general operation characteristics of a tug are known, which can be deduced based on the location and the expected job profile in that location. For the situation where general operating characteristics of the tug are known, a load prediction scheme is proposed, which is integrated with the optimization formulation for power management to determine running schedules of engines and batteries over subsequent time horizons. More technical details regarding the mathematical models and both optimization algorithms can be found in the list of references included at the end of this article.
| Acknowledgment |
Notes | References |
| The authors are pleased to acknowledge the financial contributions of the Maritime Port Authority of Singapore to conduct this research (research grant M4060926). The authors are also grateful for several insightful discussions held with Louis Kennedy and Alf Kåre Ådnanes from ABB Singapore. |
1. Gaston, J. M. (2010). Owners turn their attention to ‘Greener Tugs.’ Tugs, Towing, Pollution & Salvage. |
Ayu, A. A., Vu, T. L., Dhupia, J. S. (2013). Optimal Design of Hybrid Power-Plant Using Optimisation Techniques Applied to Electric Tugboat Power Distribution System. Tugnology’13. Vu, T. L., Dhupia, J. S., Ayu, A. A., Kennedy, L., Adnanes, A. K. (2014). Optimal Power Management for Electric Tugboats. IEEE Transactions on Control Systems Technology. Ayu, A. A., Vu, T. L., Dhupia, J. S., Kennedy, L., Adnanes, A. K. (2014). Optimal design solution for electric tugboat under current and future market trend. IEEE Transaction on Intelligent Transportation Systems. |